DV01 is equal to Notional × 0.01 % × Day Count × Discount Factor – a formula that applies to any period, any product, any derivative. **Warning**: Equation heavy!
Ever wondered why a (full) SOFR futures tick is worth $25?
Most online definitions (google searches and AI answers) spit out bond-market definitions of DV01 (the Discounted Value of 1 Basis Point (0.01%)). Interchangeable terms include PVBP (Present Value of a Basis Point), PV01 and even “oh ones”.
Why not start with futures contracts as the building block of our understanding? For a SOFR contract, every 1 b.p. change in rates changes the value of the $1m 3-month futures contract by exactly $25. That’s it.
Once you see that connection, the same logic extends to all products. Remember that swap markets are second only to futures in terms of notional traded, and DV01 is simpler for derivatives than for bonds. So here is your definitive guide to DV01 as it relates to swaps, OIS (Overnight Index Swaps), FRAs, basis, cross currency, repos and even FX.
What is DV01? The Discounted Value of a Basis Point (0.01%)
Let’s start with an equation. This describes the DV01 of a single period derivative:
Where;
- N = Notional
- 0.01% = one basis point
- DCF = Day Count Fraction. You need to know how many days there are in your period. For example, a three month period (measured on an Actual360 calendar) would have a DCF of about 0.25 (90/360), where-as a six month period will be 0.5 (hence making the longer period twice as “risky” for the same notional amount).
- DF = Discount Factor. The first three terms in the equation calculate the Value of a Basis Point. The discount factor is then necessary to bring that value back to today. It is a function of when the cash-flow is settled. Typically, that is at the end of the period (and for OIS may even be two days after the end of the period).
Building Block 1 – SOFR Futures
The easiest way to get your head around DV01 is to consider a futures contract. Why? Because futures don’t even bother with the discounting part! I like to pose the following question:
Why do CME SOFR futures have a tick value of 25?
The mathematical proof is simply a matter of plugging in the numbers to our previous equation. For a SOFR futures contract:
- N = $1,000,000 ($1m). A SOFR futures contract has a notional amount of one million dollars – see futures contract specifications here.
- 0.01% = one basis point = tick value. You don’t need to change this kids! Yes, futures contracts move in increments smaller than 0.01%, but everyone in Rates markets still uses tick values and “01” interchangeably. Get used to it.
- DCF = 0.25. They are a three month contract. Three months is a quarter of a whole year. This is not rocket science.
If you ever get confused, need to revisit DV01 or just want to test a new derivatives pricer, this is your first principle.
Why Don’t We Use Discounting to Settle Futures?
Please Remember: Futures contracts are unique in the derivatives world. The contract can only be traded on an exchange, and the exchange explicitly defines the amount of margin that they will take out of your account for a given change in price of the underlying contract.
It is these margining mechanics that makes futures work. Even though “red” SOFR contracts reference cashflows that take place next year, the exchange applies the same number of contracts x price change x $25 equation to calculate your daily margin as it uses for the front contracts.
Why Wouldn’t This Work for OIS and other OTC?
Arbitrage, my friends, arbitrage!
If someone pays me $25 today for a 0.01% move in Rates next year, I could happily take that $25 and invest it risk free. That $25 could be invested risk free for a year, at say 4%. Now imagine that nothing changes ever again. I earn 4% on my $25, it will be worth $26 in a year. And yet to settle my contract, I still only need $25. I’ve made a $1 profit “for free”, even though the market has stayed exactly the same. I hope that you can see that isn’t fair! It is risk free profit for me.
The cashflows are the same for a futures contract. But the effect of re-investing the daily margin is reflected in the price of the futures contract itself. Therefore, futures prices are not an explicit expectation of where the forward interest rate will be. They have a convexity bias baked into them.
Building Block 2 – Discount Factors
So what is the fair value to settle for an OIS that has the same characteristics as our SOFR future?
- Notional = $1m
- Start Date = T + one year
- Tenor / End Date = 3 months / T + 15 months
- Fixed Rate = 3.99%
- Floating Rate = SOFR flat, compounded daily
The net difference between the Fixed Rate and the compounded SOFR is paid on maturity date (let’s ignore settlement lags in this instance).
By calculating the DV01, we are also calculating the amount of variation margin I will pay today for each 0.01% change in the market rate of the swap. We keep things super simple and state that the market implied interest rate is a flat 4% for the next 15 months.
First, calculate the value of a basis point for this contract. Nothing here should come as a surprise:
Substituting;
And for a discount factor we use;
Where;
- DF = Discount Factor, as previously
= Zero Coupon interest rate to the end date of the swap
- DCF = Day Count Fraction. 15 months is 1.25 in our case.
DF, the Discount Factor, is therefore equal to:
…and the amount that we should settle today is .
Needless to say, we can satisfy the no arbitrage requirement by showing that;
Building Block 3 – Multi Period Swaps
Let’s now extend to a 15 month, spot-starting SOFR swap, settled quarterly.
Every period is identical, but the discount factor changes as the time to settlement of each cashflow increases. The DV01 is therefore NOT identical for each period:
| Start | End | Value of 0.01% | Discount Factor | DV01 |
| T+2 | 3 months | $1m x 0.01% x 0.25 = $25 | $24.75 | |
| 3 months | 6 months | $25 | $24.51 | |
| 6 months | 9 months | $25 | $24.27 | |
| 9 months | 12 months | $25 | $24.04 | |
| 12 months | 15 months | $25 | $23.81 | |
| Total | $121.38 |
How do I calculate a DV01 for Cross Currency, FX and Repo products?
You might be wondering how all of this relates to DV01 for other instruments, where we do not have a “Fixed Rate” to explicitly reference.
It is just as straight-forward. For a floating rate swap the cashflows still change by the same amount. 0.01% on a $1m over a three month period is the same whether we are talking about the change in a fixed rate or the change in a floating rate!
For Cross Currency Swaps, FX and Repo we are simply using a different discount curve to calculate our discount factors. Rather than using 4% in the above example, we would use 4.02% if the Cross Currency Basis was a flat +2 basis points all the way out to 15 months.
In Summary
- Question: What is DV01 in derivatives markets?
Answer: DV01, or the Discounted Value of 1 Basis Point (0.01%) measures how much the present value of a derivative changes for a 1 basis point (b.p.) move in interest rates. - Question: Why start with futures when talking about DV01?
Answer: Futures use fixed values for their tick values, providing a standardised way to introduce the simple calculations required to calculate DV01. - Question: Do you need to calculate discount factors to calculate DV01s?
Answer: Yes. DV01 is the value of a basis point multiplied by the discount factor of the settlement date. - Question: How is DV01 calculated across OIS, Cross Currency, Repo and FX trades?
Answer: The same formula applies, but the discount curve changes. For example, a +2 bp cross-currency basis adjusts the discount rate from 4.00 % to 4.02 %.

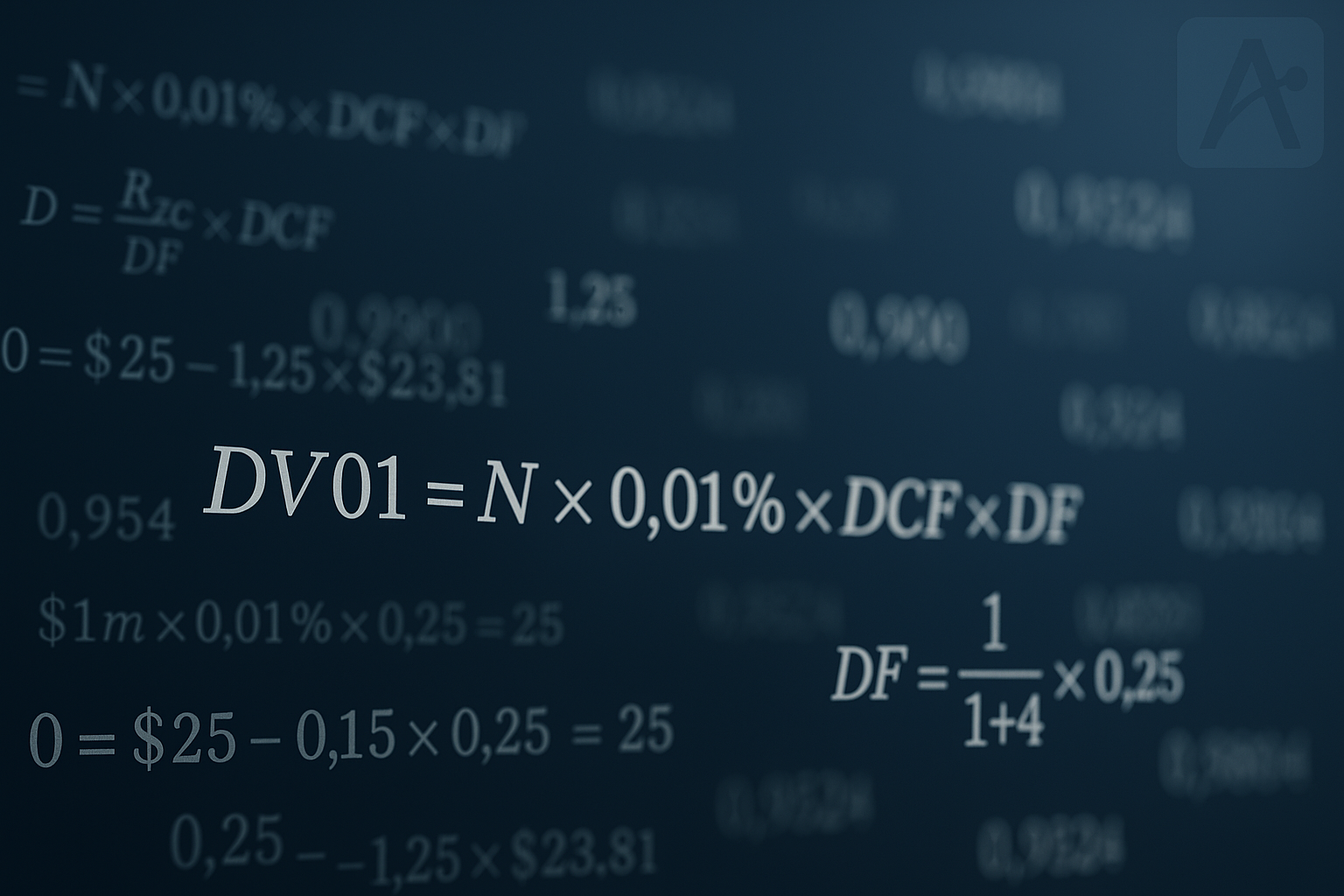
Leave a Reply