Bond futures, conversion factors, cheapest to deliver bonds. Let’s unpack some terrifying-looking equations into simple high-school mathematics.
Ever wondered where the conversion factor for Gilt futures comes from?
The contract specs for bond futures contracts read like a PHD in astro-physics wrote them (they probably did!). They include statements like;
“Imagine a hypothetical ten year bond paying a semi-annual coupon of 4%.”
Great – my starting point appears to be an imaginary financial instrument. I am not off to a great start. Let’s try again.
“One Gilt future allows a market participant to lend (or borrow) £100,000, at a semi-annual fixed rate of 4% for a period of ten years.”
This blog covers derivations of the tick value, the DV01, the conversion factor and the cheapest to deliver. Knock yourselves out!
Building Block 1 – Build the Cashflows
What does this contract look like in terms of cashflows? Using the same principles as I explained in the articles on DV01 and Easy Swap Pricing, we can create the exact cash-flows of the Gilt Future from the one-line description above:

For Gilt futures (unlike SOFR futures), the price tick is not equal to the DV01. The Gilt Future contract is instead defined as having a minimum price move of 0.01 per £100. The price that you are committing to pay for these cashflows is therefore changing by only £10 per futures tick:
Where;
= Tick value of 1 Gilt Future.
- 100 and 100.01 represent the smallest possible price moves of the future (minimum price fluctuation on the ICE website).
- The prices are divided by 100 because the price quotation is per £100 nominal.
Building Block 2 – Discount the Cashflows
As we examined in previous blogs, we do not receive all of those cashflows today. We receive them at different times in the future. Because those cashflows arrive at different times, we expect to be able to invest them at different interest rates throughout the life of the contract.
Using the methodology from Simple Swaps Pricer, I built myself a hypothetical SONIA curve (these are not actual market prices):

These daily forward rates allow me to calculate a SONIA Index value for any date in the future;
- SONIA Index Value is calculated as;
Where;
= SONIA rate fixed on date A.
= Day count fraction calculated as Actual 365F between dates A and B.
Which in turn is directly translated into daily Discount Factors (DF) using;
This allows me to see the Net Present Value (NPV) of the Gilt Future cashflows:

Showing;
- If you sum all of the cashflows on a Gilt Future they should be £40,000 (4% annually on £100k for 10 years).
- Using a hypothetical SONIA curve, I calculated the NPV of those same cashflows as ~£11,000.
Building Block 3 – The Value of 1 Basis Point
In equation form, recall from the DV01 blog that;
Where;
- N = Notional. For a Gilt future, this is £100,000.
- 0.01% = one basis point
- DCF = Day Count Fraction. You need to know how many days there are in your period. For a Gilt future, this is calculated on an Actual/Actual calendar.
- DF = Discount Factor.
We so far understand that:
- 1 futures tick (0.01) is worth £10.
- That a 0.01% change in the cashflows of a single Gilt Future is equal to £100.
- That the cashflows of a Gilt Future amount to about £40k, but have a discounted value much lower than this – about £11k on my curve.
We now want to know what the DV01 of our Gilt Future is. Turning to our lessons from the Simple Swap Pricer, it is all linear mathematics again:
- Calculate the discounted value of your cashflows using the SONIA Index built above.
- Calculate a new SONIA Index for each date. This is the same formula, but with each SONIA fixing set higher by 0.01%.
- For example, a SONIA fixing of 3.9693% becomes 3.9793%.

What does this tell us?
- If our SONIA curve moves by 1 b.p. then the value of a single Gilt future will change by £94.10.
- In other words, the number of futures ticks that has the same £ impact as 1bp on the swap is 9.41.
- This will change, depending on the outrate level of rates. I used a hypothetical SONIA curve with a 10 year break-even around 2.7%. Your results will vary depending on your market data.
- This ratio is therefore helpful, but only if you are pricing a 4% swap (and at the discount curve I used)!
- What I really want to show is the hedge ratio that swap traders use. This is the number of futures contracts for a given swap DV01.
- That leads us to Conversion Factors and the Cheapest to Deliver bond.
Building Block 4 – Cheapest to Deliver
The Long Gilt future is a contract to settle 10-year 4% semi-annual cashflows, with most contracts closed-out before expiry. Yet it can also be settled by delivering an actual bond. There is a deliverable basket of eligible Gilts, with different maturities (from 8.75 years to 13 years) and of different coupons (currently from 0.625% to 4.5%).
To work out which is the “best” (read cheapest!) Gilt to hypothetically deliver, we need to discount the cashflows of each of the eligible Gilts. We discount all of the cashflows (coupons, accrued interest to the delivery date and the final redemption amount) at a flat 4% yield curve – this allows us to calculate a market neutral conversion factor per bond.
If you’ve built the spreadsheet already, you can easily create a SONIA curve that fixes at 4% each day, complete with daily discount factors. Here’s a coupon-by-coupon example for the 4.5% 2034s:

Helpfully, futures exchanges publish these conversion factors. This standardises everything, and prevents differences cropping up between market participants (for example, my DCFs are slightly off for Gilts above). For ICE, the conversion factors can be found here.
The exact equation that ICE use is shown below.
Where;
- x = notional interest rate; i.e. 4% for the Long Gilt future at ICE.
- r = days of accrued interest for underlying Gilt
- s = days in current coupon period for underlying Gilt
= current semi-annual coupon of underlying Gilt
= next semi-annual coupon of underlying Gilt
- c = annual coupon of underlying gilt
- n = number of full coupon periods from next coupon until redemption of underlying Gilt
- AI = Accrued interest
This adjustment makes every deliverable bond economically equivalent to a strip of 10-year 4% cashflows at the notional yield. The conversion factor is defined so that, at a flat 4% yield curve, each deliverable bond would be equally economic to deliver. When actual yields differ from 4%, differences emerge – giving rise to the Cheapest to Deliver.
The Cheapest to Deliver (CTD) Gilt in the basket of eligible bonds is the bond that minimizes the invoice price:
(It also maximizes the implied repo rate (because you are buying back the cheapest bond), but I don’t want to get into the basis trade in this blog).
Building Block 5 – Hedge Ratios (Swaps vs Futures)
Using the published ICE Conversion Factors, and the current price of the Gilt Future at 93.47, it is the 0.625% 31/07/2035 Gilt that is the cheapest to deliver.
Swaps traders project the gilt cashflows of the CTD onto the same curve as their swaps. I am holding the futures price constant, but revaluing the CTD cash-flows on my SONIA (discount) curve. This makes the DV01 directly comparable with a swap DV01.
Plugging the CTD details into the swaps pricer tells us that the DV01 per contract is £77.21 on my hypothetical SONIA curve:

Compare this to the DV01 of a spot-starting 10 year IRS. I do this by duplicating the above pricing grid, but with two legs (Fixed and Floating). The rate between any two dates was defined in the Simple Swap Pricer blog as:
Where;
= SONIA Index at the start of the period.
= SONIA Index at the end of the period.
= Day count fraction calculated as Actual 365 between the two dates.
On my SONIA curve, I have a 10 year break-even rate of 2.72%. This gives me a DV01 of £88.65 for a spot starting 10 year SONIA OIS:

As a result my Futures:Swap hedge ratio is;
That tells me how many Gilt contracts I need to buy or sell for each £1 of swap DV01 I am trying to hedge.
In Summary
- Question: What are the cashflows of a bond future?
Answer: One Gilt future allows a market participant to lend (or borrow) £100,000, at a semi-annual fixed rate of 4% for a period of ten years. - Question: What is the tick value of a bond future?
Answer: For Gilt futures, it is 0.01 per 100 face value on a notional of £100,000 = £10. - Question: What is the DV01 of the bond future?
Answer: We project the cashflows of the future onto a SONIA curve and show you how to calculate the DV01 using the ratio of two indices. - Question: What is the conversion factor?
Answer: An adjustment to the futures price that makes every deliverable bond economically equivalent to a strip of 10-year 4% cashflows at the notional (4%) yield. We derive the calculation. - Question: What is the Cheapest to Deliver (CTD) bond?
Answer: The bond with the lowest invoice price on the delivery date, when taking into account conversion factors and accrued interest. We derive it. - Question: What is the Swap:Futures hedge ratio?
Answer: Once we know the cashflows of the CTD bond, we derive the DV01. We compare the DV01 of the Gilt Future with the DV01 of a spot-starting 10 year SONIA OIS on a hypothetical SONIA curve.

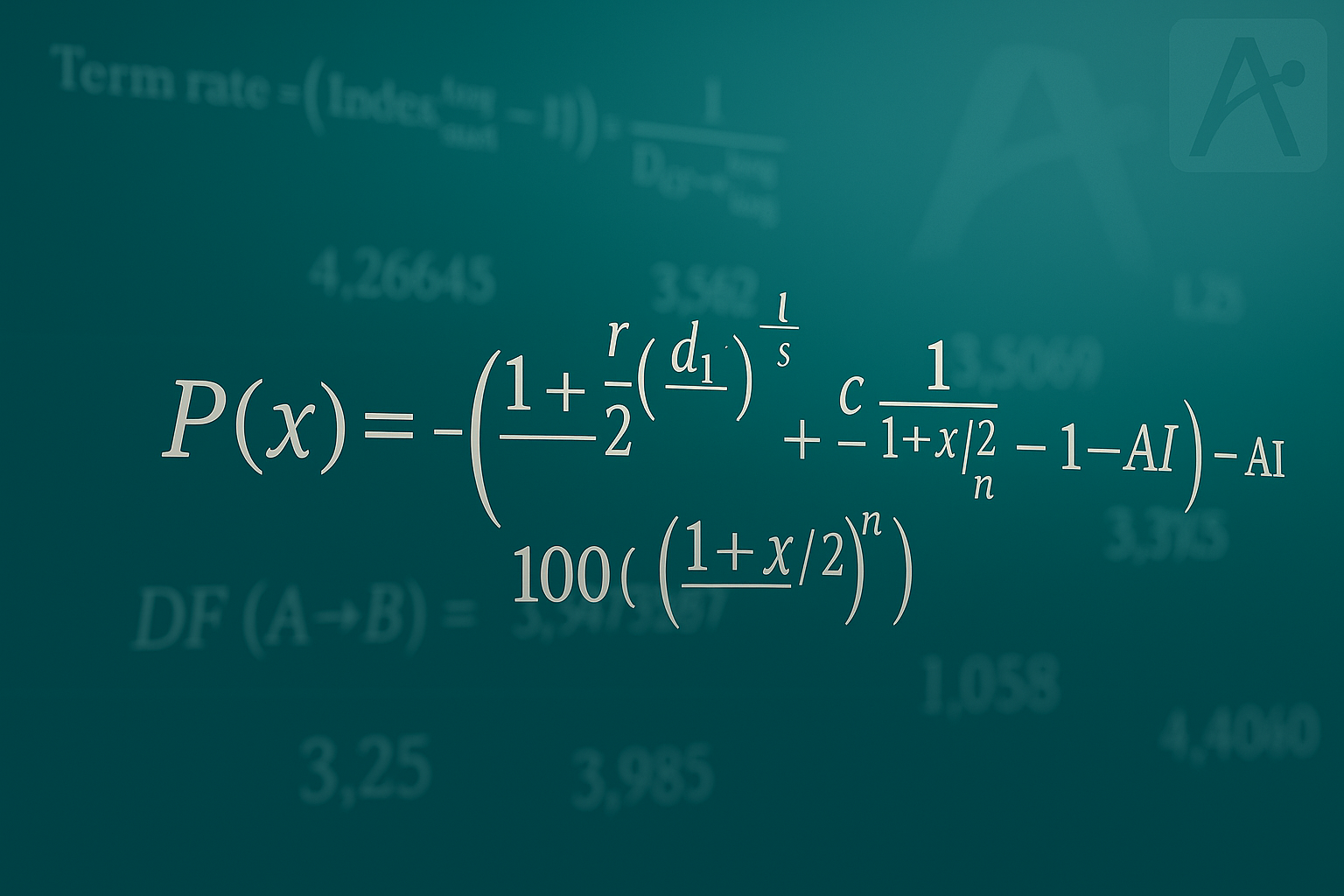
Leave a Reply